Preface
上一节主要内容是在没有Model的情况下如何去做Policy Evaluation,本章的重点是要没有Model的情况下去学会做决策,下一章将会介绍Value Function Approximation。学会优秀的策略需要应对以下两个问题,首先是Delayed Consequences,也就是说当前的决策可能需要在未来好几步才能够反映出好坏和价。其次就是要做到适当的Exploration,因为需要进行适当量的探索才能够发现较为优秀的策略。
对于许多的MDP模型来说,以下两种问题需要我们使用Model-free Control去解决:
- MDP model is unknown but can be sampled.
- MDP model is known but it is computationally infeasible to use directly, except through sampling.
On-policy learning 和 Off-policy learning是两种学习的方法,前者在和环境的交互中直接进行学习,也就是当前的policy和当前的sample是对应的;而后者能够从另一个不同的policy中去进行Evaluation和参数的更新。
Generalized Policy Iteration
首先回顾一下PI的流程(此时的PI是有真正Model的):初始化一个policy$\pi$;重复以下两步操作,首先进行Policy Evaluation,然后利用$\arg \max_{a} Q(s,a)$对当前policy进行更新($Q$值计算用到了$P$);直到拟合。在Model-free的情况下PI的流程也是一样的:重复Policy Evaluation + Policy Improvement。只是Policy Evaluation现在需要进行estimate Q来得到。
MC for On-policy Q Evalution
- Initialize $N(s,a)=0, G(s,a)=0, Q^\pi(s,a)=0, \forall s \in S, \forall a \in A$
- Loop
- Using policy $\pi$ sample episode $i=s_{i,1}, a_{i,1},r_{i,1},s_{i,2}, a_{i,2},r_{i,2}, \dots, s_{i,T_i}$
- $G_{i,t}=r_{i,t}+\gamma r_{i,t+1}+ \gamma^2 r_{i,t+2}+ \dots + \gamma^{T_i-1}r_{i,T_i}$
- Foreach (state,action) $(s,a)$ visited in episode $i$
- For first or every time $t$ that $(s,a)$ is visited in episode $i$
- $N(s,a)=N(s,a)+1, G(s,a)=G(s,a)+G_{i,t}$
- Update estimate $Q^\pi(s,a)=G(s,a)/N(s,a)$
- For first or every time $t$ that $(s,a)$ is visited in episode $i$
在此estimated Q value的基础上,我们只需要更新policy为:
这样的estimation可能会有一些问题,例如如果$\pi$是deterministic的或者对某些action的probability为0,那么我们就没有办法计算$Q(s,a)$ for any $a \neq \pi(s)$,这是由于我们在sample时不会采样到其余的action。并且我们希望对于Q值的estimation和policy improvement能够相互穿插,而不是现在的大量的estimation的sample和更新得到一次policy的参数更新。这些内容会在下文中cover。为了平衡exploration和exploitation,一个简单的想法就是使用$\epsilon$-greedy方法。
这里可以证明:For any $\epsilon$-greedy policy $\pi_i$, the $\epsilon$-greedy policy w.r.t $Q^{\pi_i}$, $\pi_{i+1}$ is a monotonic improvement $V^{\pi_{i+1}} \geq V^{\pi_i}$ .证明过程略去,给出笔记中的截图。

Greedy in the Limit of Infinite Exploration (GLIE)
$\epsilon$-greedy策略是能够让每次策略更新依旧保持单调增长的一种方式。而我们可以对这个策略进行适当的refine从而让这种更新策略保证收敛。GLIE的定义由以下两个条件组成:
首先,所有的state-action对被访问的次数在sample次数的数量趋向于无穷时也应当趋向于无穷:
第二,当sample数趋于无穷的时候,policy选择Q表中最优值的概率应当趋于1.
一个满足GLIE条件的例子就是让$\epsilon$-greedy探索的随机性系数$\epsilon$随着sample的样本改变:$\epsilon_i = 1/i$. 同时GLIE Monte-Carlo Control能够确保收敛到Optimal的state-action value function:$Q(s,a)\to Q^*(s,a)$.
Monte Carlo Online Control
结合上面的内容,在线的MC Control算法可以用以下的伪代码表示:

Temporal Difference Methods for Control
通常情况下使用TD方法进行Model-free PI的框架可以被归纳为:随机初始化策略$\pi$;重复更新策略(和使用MC方法几乎相同)Policy Evaluation + Policy Improvement。
SARSA
SARSA算法的伪代码如下图所示,和MC方法的核心变化在于TD方法不需要等一个episode完结才能够进行更新,而是根据下一个step的观察可以直接进行更新,其依据就是利用Bellman方程的estimation:

SARSA for finite-state & finite-action MDPs 在以下两个条件成立时能够保证收敛到最优的action-value:
- 策略序列$\pi_{t}(a | s)$满足上面所提及的GLIE条件
- 步长$\alpha_t$满足Robbins-Munro序列要求:
- $\sum_{t=1}^{\infty} \alpha_{t}=\infty$
- $\sum_{t=1}^{\infty} \alpha_{t}^{2}<\infty$
在实践中我们的步长一般不遵从这里的限制,通常使用的是逐级递减的步长就可以。这里提到了SARSA采用的更新策略是实际sample出的下一个step的情况,这种方式对比Q-Learning来说是“相对客观”的。Q-Learning会过分乐观(因为更新策略中拿到的是max value),但是SARSA算法在Sutton and Barto的cliff walk example中表现会更好。关于这个问题,我们会在这章最后简单用代码实现一下。但是很多的问题都不会具有这样的性质。
Q-Learning
Q-Learning也是一个Temporal Difference的方法,和SARSA相比,Q-Leaning不需要从policy当中sample出确切的action,而是更新时采用当前时间步最大期望的action-state值进行更新,因此Q-Learning也被认为是一种off-policy的算法。虽然理论上Q-Learning能够确保收敛到和SARSA一样的最优值,但初始化的状态也依旧会产生一些影响。总体来说,optimistic initialization会比较有帮助。以下是两种算法更新函数的比较。
- SARSA:$Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left(\left(r_{t}+\gamma Q\left(s_{t+1}, a_{t+1}\right)\right)-Q\left(s_{t}, a_{t}\right)\right)$
- Q-Learning:$Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left(\left(r_{t}+\gamma \max _{a^{\prime}} Q\left(s_{t+1}, a^{\prime}\right)\right)-Q\left(s_{t}, a_{t}\right)\right)$

Maximization Bias
课程笔记中举了一个扔硬币的例子:


为什么会导致这样的偏差?原因在于我们将estimate的过程和control的过程放在了一起,导致了对于结果过于乐观的估计。在扔硬币的例子中为了回答第二个问题我们其实完全可以重新estimate选择出来的硬币,这样就可以避免了这样的bias。那么通过这个经验,我们就可以将estimation和control的过程进行分离从而保证估计的无偏性。
关于这个问题的更加数学化的例子:

为了解决这个问题,研究者找到了Double Q-Learning算法。简单来说就是采用一个Q-function来进行estimation,另一个Q-function进行action sampling。以下为Double Q-Learning的伪代码:

这种方法使用了independent samples to estimate the value。而在现实中使用该算法时,可以以0.5的概率对这两个Q function进行交替的estimate和sample。Double Q-Learning只增加了内存开销,不会产生更大的计算开销,而且能够达到非常好的效果。以下的实验结果告诉我们Q-Learning在前期非常可能suffer在不是最优的策略中,但Double Q-Learning却能够很好地解决这个问题。
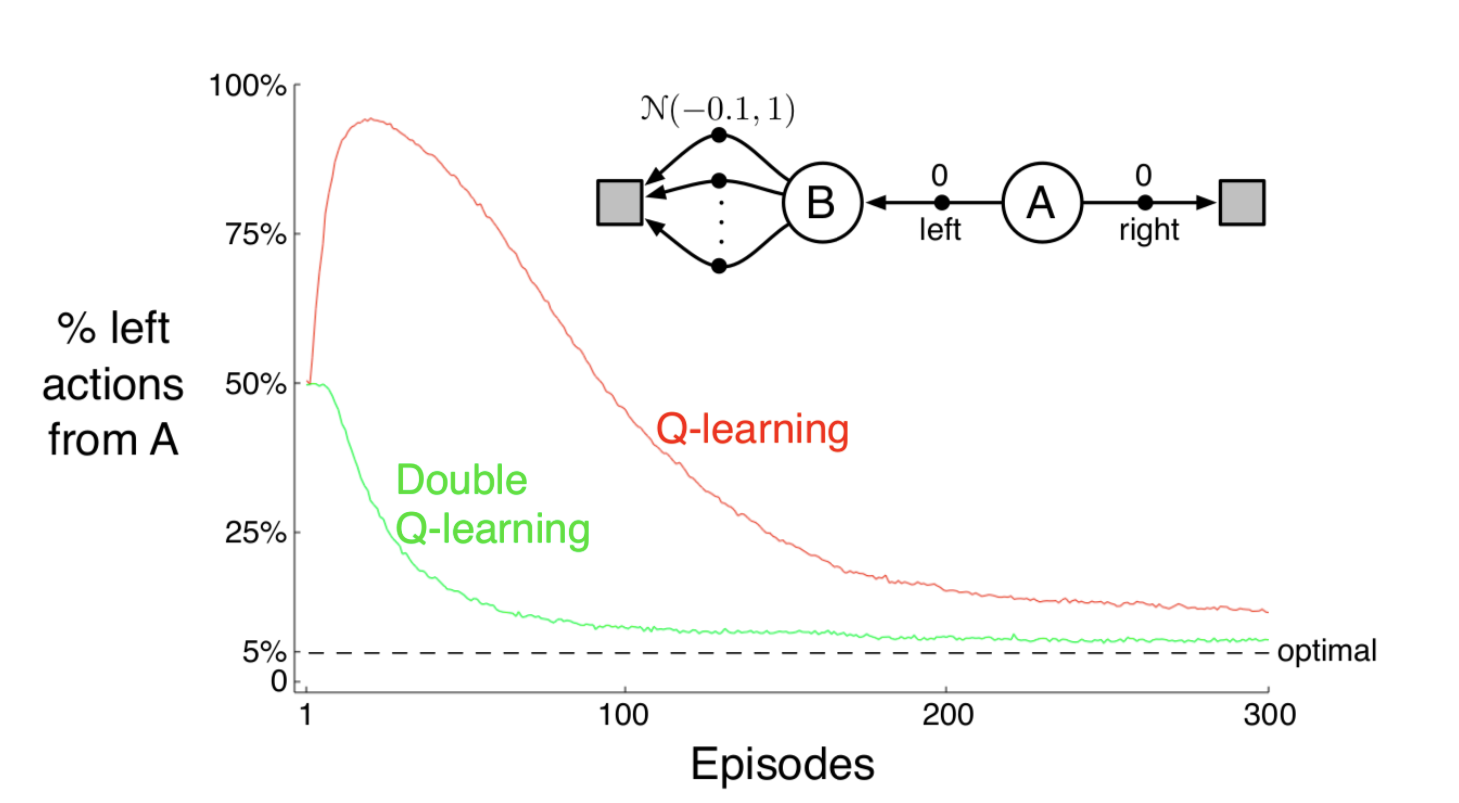
这篇博客对这个问题进行了一些阐述,最主要的观点是Q-Learning中的max函数导致了过于乐观的估计。如果Reward带上了随机性(例如遵从一个EV为负的分布),那么sample前期的正向结果都会导致模型得到错误的估计,估计导致策略向这个错误的方向偏移,会使得模型在未来的一段时间内都得出不好的结果。
What is happening here is that, if an action’s value was overestimated, it will be chosen as the best action, and it’s overestimated value is used as the target. Instead, we can have two different action-value estimates as mentioned in the above equation, and the “best” action can be chosen based on the values of the first action-value estimate and the target can be decided by the second action-value estimate. How do we train though?
Divide the samples into two halves. For the first half, we can use the above equation to train, and for the second half swap the “1” with the “2” in the equation. In practice, data keeps coming into the agent, and thus a coin is flipped to decide if the above equation should be used or the swapped one. How does this help?
Since the samples are stochastic, it is less likely that both the halves of the samples are overestimating the same action. The above method separates two crucial parts of the algorithm, choosing the best action and using the estimate of that action, and hence works well.
虽然我们仅仅是在非常简单的场景当中阐述了可能产生maximization bias的可能情况,也有研究者指出在Atari这样复杂的游戏中也会产生这样的问题。而同时,如果所有的action-values都受到了overestimation的影响,那么对于最终学习到的策略不会有任何影响;相反,如果不同的state所受到的影响不同(例如有些state的reward是恒定的),那么对最终的optimal policy会产生影响。